In conformal geometry, a hyperbolic glide reflection has a circle as one of its invariants. This is the fact being exploited when someone says “in Conformal GA, a circle is the wedge of three vectors” - a very misleading simplification that has become foundational to CGA. For the purposes people use it for, it does work beautifully, and in any number of dimensions - that means it is not to be sniffed at. Here’s why it works.
Glide reflections

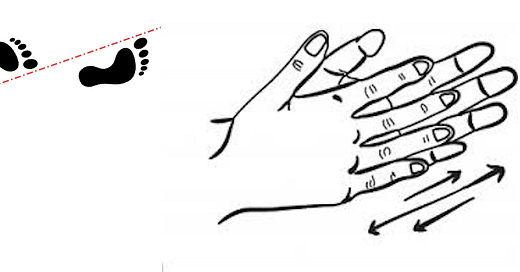
Glide reflections are what you get when you concatenate a reflection and a simple motion, like the “move forward” euclidean motion in this first picture. I’ve previously talked about rotoreflections, which is a glide reflection where the motion is a rotation. These things matter because they’re the a low-dimensional first-taste of something that proliferates hugely in higher dimensions: combinations of transformations, where the combinations have subtleties you need to keep on top of.
A subtlety that glide reflections illustrate well is that if there’s a single transform that is a reflection followed by a motion, the motion must commute with the reflection, which constrains both of them. With the footsteps, you’re walking along the reflection line; with the hand rubbing, you’re moving in the reflection plane.
Glide reflections that are hyperbolic
Chris Jerdonek has done an incredible job of animating 2D hyperbolic isometries - I strongly recommend taking a glance at that page to clarify your understanding! Here are his hyperbolic glide reflections (hereafter: HGRs).
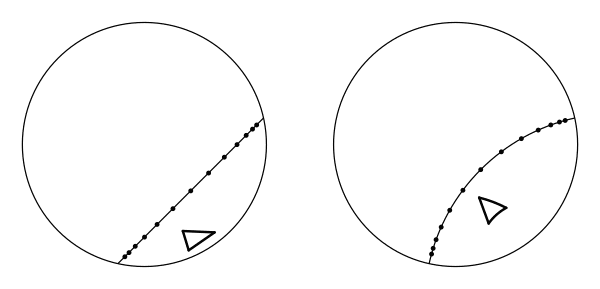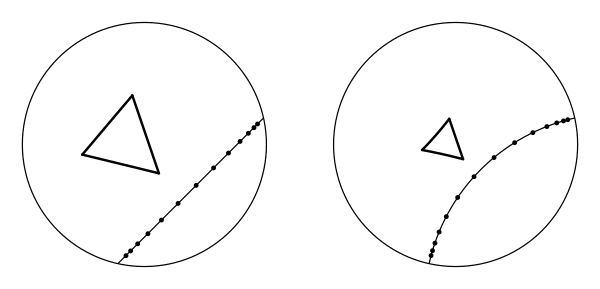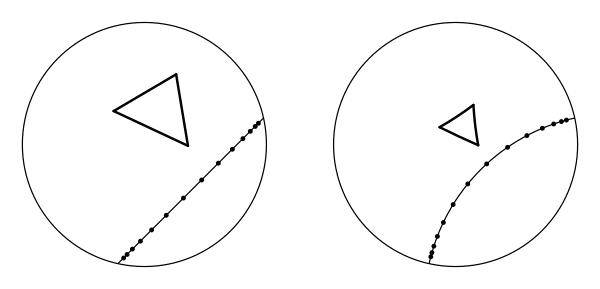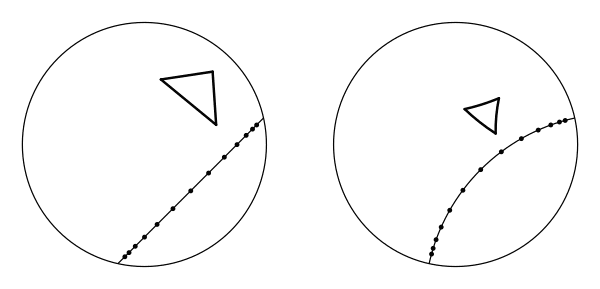
Again, that’s a reflection followed by a motion - in this case a hyperbolic motion. The reflection is in a hyperbolic “line” (lines can look like circles), and the motion is along it.
Here’s a HGR in 3D:

Even in one dimensional CGA, which has the signature Cl(2,1), you have hyperbolic glide reflections!
Geometric product versus wedge product
People learn CGA with the wedge product. Let’s review the incorrect things that causes them to believe. They’re told points are precisely null 1-vectors; the wedge product is precisely the join; the wedge of two vectors is precisely a point pair (bivector); the wedge of three vectors is precisely a circle (trivector).
Spending any time thinking about CGA’s transformations will make you doubt this simple story. An example I like is the fact that it is possible to rotate around a circle:

A rotation around a circle (“toroidal vortex”) is scalar+bivector in 3D CGA. The bivector specifies the circle. It’s also the composition of two sphere reflections, so long as the spheres intersect - in this case the bivector will be, precisely, the circle where the spheres intersect, eg their wedge product.
The wedge product is not the “join”. Nor is it the “meet”, as you might think from “sphere-based” CGA.
The wedge product of some things is the highest-possible-grade-blade in the geometric product of those things. The geometric product is transform composition. And the highest grade part of a transformation is its most specific invariant. That means the meet and the join can be a wedge product:

HGRs are to trivector-circles what quaternions are to bivector-lines
Imagine an alien in a different universe. They’re unfamiliar with the idea of “3D rotations”. They’re looking into these “quaternions” that humans use to model their transformations. They notice quaternions are scalar-plus-2-blade. They’re lazy so they look at just the 2-blade part. The 2-blade quaternions do 180 rotations. They conclude all rotations are 180 degree rotations. They maybe don’t even conclude that “angles” are possible at all.
We want to say to the aliens: “no, don’t stop there! We can do rotations by 10 degrees and 45 degrees! To get those, you have to take the grade 2 blades and add them to a multiple of the identity to reduce the angle”.
That’s what I want to say to CGA practitioners. You just can’t learn this stuff if you only use the wedge product and think about blades, because hyperbolic glide reflections are not blades - except for, I suppose we have to say, “degenerate” hyperbolic glide reflections consisting of only reflections.
Take an example: 2e1 + e12- is a HGR. e12- is a blade that is a component of it. Standard CGA focusses on e12- on its own.
What is e12-? On its own it appears to be a circle reflection (with some strange parity stuff! Will remark on this in a second).
But it’s bad to stop at “what can this blade do on its own?”. We must instead ask: what are the transformations that are close to e12-? Or to put the same statement another way, “if I chain some reflections together and get an transformation whose trivector part is e12-, what will that transformation be?” - that’s the question that HGRs answer. 2e1 + e12- is a reflection of e1 followed by a hyperbolic motion of 2 + e2-. That’s the equivalent of the alien learning about angles.
And it’s especially important to inquire into this stuff with Conformal GA, because e12- is not the only thing that’ll do that circle reflection - its dual will do the same circle inversion but e12- and its dual are different objects!:
e12- is involved in a family of HGRs, each of which can be gotten by adding it to multiples of specific 1-vectors
In 3D CGA, the dual of e12-, which is e3+, is involved in a family of rotations, which can be gotten by adding it to multiples of the identity
Both of these families are important conformal transformations. And without understanding them you cannot say you understand conformal transformations. Which is our one and only goal with CGA, since the practical case for it is so weak!
Alright, the parity thing. e12- has the property that if you multiply it by its reverse (take its “spinor norm”) you get a negative number; thus to apply it to an object will get in some sense the “negative” of that object. That’s not true of its dual; and to be frank, this sort of tells you e12- shouldn’t be considered as a transformation in isolation at all, but instead only seen when it is added to an appropriate 1-vector as in e1 + e12-. To say it more formally: conformal transformations should be studied using Pin+, which is the products of 1-vectors that square to 1.
If you’ve made it this far, you might start to see why, when talking about CGA, I like to say “reflection-sphere” or “rotation-line”; there are “hyperbolic-glide-reflection-lines” as well! And in the context of CGA there’s really no such thing as a “line” independently of involvement in a rotation or an HGR.
HGRs in the projective view of 2D CGA
You’re done now, but there’s the “projective view” of CGA is important; I have a long video about it. Here’s what HGRs look like there:

I was explaining recently how trivectors and 1-vectors in 2D CGA can be circles. These trivectors that are points-outside-the-klein-3-ball cast “shadows”, in some sense, on the klein 3-ball - they’re made of all the lines tangent to the sphere that pass through the point. HGR trivector circles are as distinct from 1-vector circles as planes are from points!
By the way, the points you see there are the “pointors” of 2D CGA.
So for those wanting an explicit algebra statement, in an HGR:
There is a 1-vector part, which alone would square to a positive number proportional to the cosh of the hyperbolic distance
There is a trivector part, which alone would square to a positive number as well, proportional to the sinh of the hyperbolic distance
The two will have zero wedge product