Sphere, circle, and cylinder intersections in Projective Geometric Algebra (are easier than in Conformal GA!)
The following formula does circle-line intersection in 2D Projective GA. Normalized line L, circle center point (also normalized) and radius (P,r):
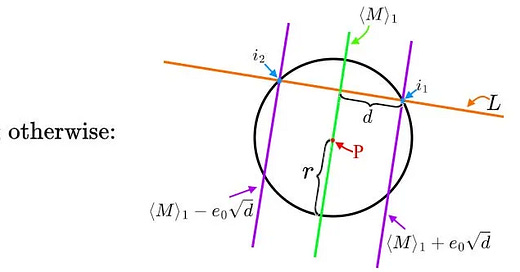
Alright, now time for sphere-line intersection in 3D. Normalized line L, sphere center point (also normalized) and radius (P,r):
Hmm wait a second, that’s the same. Yes, it is, all the way down to the grades of the objects you extract. In 3D PGA, lines are grade 2 (instead of 1) and points are grade 3 (instead of 2), but the math works out the same.
Something that would be nice would be line-cylinder intersection - you could use that for a bunch of things in gamedev. First let’s consider the intersection of an infinite cylinder with a plane that is parallel to its axis. Note that its intersections will be lines. Plane P, cylinder axis A (again both normalized), cylinder radius r:
That’s a bit unlikely to want, but it’s helpful in what follows.
Intersection with a line and an infinitely long cylinder. Line L, cylinder axis A (normalized…), cylinder radius r:
EDIT: almost two years later, a bonus: finding the closest point on a cylinder to a point.
We represent the cylinder with a height and radius values, and an axis A - and a plane that bisects it, P. We have a point p and we want to find the closest point to p on the surface of the cylinder.
P·p is the line through p parallel to A
A·p is the plane through p parallel to P
d₁ := ||★(P·p-A)||
d₂ := ||★(A·p-P)||
X := A + (P·p-A) * min( 1, radius / d₁ )
Y := P + (A·p-P) * min( 1, height * 0.5 / d₂ )
… and the answer is X∧Y. X is the line parallel to L that is as close as possible to passing through p while still intersecting the cylinder; Y is the plane parallel to P and as close as possible to passing through p while still intersecting the cylinder.
Using P we can get the caps in our line-cylinder intersection. Take L∧(P±e0*height/2), which are the intersections with the planes of the caps, call them i₃ and i₄. The cylinder intersections are whichever elements of {i₁, i₂, i₃, i₄} are such that ||(i/||i||)∨A|| < radius and ||(i/||i||)∨P|| < height * 0.5.
Conclusion
A CGA fan might say: “CGA has a representation of not just lines but circles - so you can take the intersection of a plane and a circle or a sphere and a circle (and projections onto circles etc)!” - but I don’t see much use for this in graphics. I would be interested to be corrected on this.
A CGA fan might say: “Instead of these 4 lines of code, CGA gives you line-sphere intersection in one line of code!” - as a person who just wrote a paper on point pairs and other CGA objects, take it from me, you don’t want to have to deal with them. As a graphics programmer you have to extract the points from the pair anyway, with code which, at best, is equal to the clarity of the above - and that’s a real stretch, because bear in mind that one of the points could be at infinity.
A CGA fan might say: “Well, how about if the sphere and line don’t intersect? CGA gives you an answer anyway, which could give you useful information”. Here again I would be interested to see an example use case for that information. The potentially-useful information would include the distance of the line from the sphere - that could be good for, say, calculating shadows or the next step distance in a ray march. But I’d be amazed if the distance were in that result in an easy-to access form. If it was, I’d expect it to have been mentioned here. If that turns out to be the case, it’ll be a bit like how PGA fans like to say that our line-plane intersection solution is way better than traditional vector algebra because we handle the situation where the two are parallel; to which some people might say “yeah but that is an exceptional situation”; but in that situation, you do get the distance dropping out of the result in a useable form, and you get a meaningful “direction” of intersection too, which you may well want.
I really like how the above use the geometric product and transflections. It’s a classic case of starting out with two geometric objects (line, sphere/circle/cylinder) and wanting to know two things about their relationship. And it turns out that the geometric product of PGA, almost magically, gives you the objects that you want, scaled by the measurements that you want. And that’s a transflection, which on the face of it you’d have thought would be not-that-useful. Even <M>₁ comes pre-normalized, because that’s how transfections work.