How to extract points from point pairs in Conformal Geometric Algebra

Because for some reason you're doing Conformal GA instead of Projective GA, you complete and utter maniac.

Don’t do conformal geometric algebra unless you’re sure you need to. Most engineering is about euclidean space, where you care about distances, translations, ordinary rotations and so on. For this, the correct thing to use is Projective Geometric Algebra (even if you are thinking about sphere and circle intersections) - Conformal GA is awful for euclidean geometry. If you don’t already know this, consider the length and complexity of this post to be one of many arguments to that effect!

Ok, you’re still reading. You really want to do Conformal GA - I suppose you’re interested in geometry generally, or perhaps you want to do conformal animation, or perhaps you’re a physicist interested in the nature of causality via Twistor theory (conformal GA for space-time). I hope you’re ready for a journey that’ll take you through some weird quantum-physics/representation-theory/Bohmian philosophy adjacent algebra.

My approach here is based on Joan and Anthony Lasenby’s guide to CGA - but is different because their approach fails in the highly likely situation where one of the points is the point at infinity.

Point pairs as transformations

“I don’t want to think about transformations (versors), I just want to think about geometric objects (blades)”, you say, “can’t you just give me the formula already?”.

Scroll down if you want. The algebra is not even difficult, as such. You’ll come crawling back to this section in a few months though. Transformations are necessary if you want to know the truth about CGA.

Anyway, here’s Eric Lengyel’s depiction of two different point pair transformations in 2D CGA Cl(3,1,0):

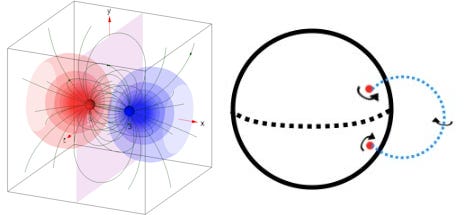
Here’s what they can be like for 3D CGA Cl(4,1,0), with the left one coming from Marianne Breinig and the right coming from this post of mine:

And here’s 1D CGA, Cl(2,1,0):

As you see, there are always two qualitatively different sorts of (simple) transformation that are defined by the point pair. That’s so for any number of dimensions (and for quantum physicists in the audience: these transformations always commute).

One of those transformations (the ones on the left for 2D and 3D, and the one on top for 1D) is always a transformation that is represented by a bivector that squares to a positive number. It is the one which pulls away from one point and pushes towards the other; they’re called hyperbolic translations and they exist in any number of dimensions. They’re what we’ll use to extract points from point pairs.

You might have the other kind of point pair. For example if you’re doing 3D CGA you might have the kind on the right, which is grade 3; in 1D you might have the green one below, which is grade 1. To go from these to a positive-square bivector, you just have to dualize (yuck).

Understanding zero-radius spheres as tangent planes using stereographic projection

Haha you thought you were done learning Weird Geometry, that was nothing.

Famously, CGA has sphere(-reflection)s. A little clarification there: in 2D a “sphere” is a circle and in 1D it is a point pair (like the green point pair on the black line above).

CGA also has, and frequently uses, zero-radius-spheres. These differ from points in the strict sense because, for example, a zero radius sphere can have a zero radius circle embedded in it; a point can’t have that. If this doesn’t make sense, think about it until it does! We’re wanting to extract points from a point pair, and it turns out that what that really means is extracting zero-radius-spheres from a hyperbolic translation.

Zero-radius spheres in CGA all square to 0. Does the converse hold - i.e. if a sphere squares to 0, is it definitely zero-radius? The creepy answer is no; there is exactly one other sphere which doesn’t; that’s the sphere at infinity.

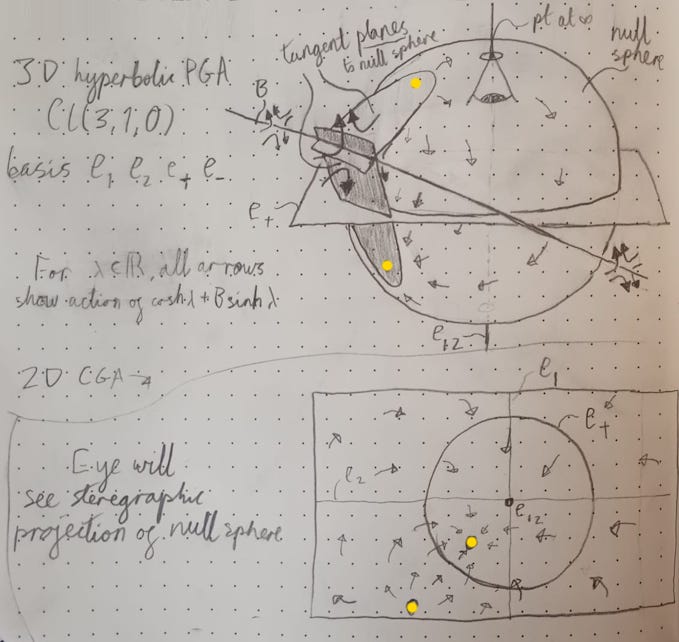
To make sense of this, we understand CGA with stereographic projection. Stereographic projection is what you see if you put your eye at the north pole of a sphere and imagine that you can see only the surface of the sphere:

In the lower picture there are three circles. But the circles are “actually” planes cutting this sphere. Well, “cutting”. The tiniest one is tangent to the sphere - it is a zero-radius circle.

To understand the “circle at infinity” thing, imagine a zero-radius sphere tangent to the north pole - to the eye, that would be an infinitely large circle. If that seems weird, perhaps imagine taking the equatorial cutting plane and imagine slowly moving it upward, to the north pole - what would that action look like to the eye at the north pole?

Hyperbolic translations using stereographic projection

Alright, you know what CGA’s circles look like with stereographic projection. What does our important tool, the hyperbolic translation, look like? Some animations of them are below. Let me be very clear: these are animations do NOT show CGA, they show the Klein disk and Klein ball models of 2D and 3D hyperbolic geometry, which is modelled with hyperbolic PGA, not CGA.

So if these animations are not showing CGA, how can we connect it to them?

It turns out the 2D hyperbolic animation has 1D CGA is on its boundary! Put your eye at the north pole (and don’t move it) and imagine you see only the rim of the circle - your eye is seeing 1D CGA.

Same with the 3D one - put your eye at the north pole and imagine you can only see things as they cut the surface of the sphere. That is 2D CGA.

Both these animations show rotations then hyperbolic translations. And you’ll notice the hyperbolic translation part, in both cases, preserves a pair of points on the surface of the circle/sphere!

Here’s the hyperbolic translation of 1D CGA from before, with the stereographic view included, and e₁ and e₊ as coordinates:

And here’s the 2D case from Eric’s picture:

Stare at the sphere with the eyeball at the north pole, and the circle with the eyeball at the north pole, until you see their connection to the animations. You should be able to make sense of these statements:

1. A hyperbolic translation is defined by an axis one dimension higher

2. The axis is incident with exactly two special hyperplanes (hyperplanes are lines in 2D and planes in 3D). These hyperplanes are tangent to the null sphere.

3. On the null sphere, the points of tangency are the apparent origin and destination of the hyperbolic translation

The solution

Alright - for a positive-square bivector B, its two points p₁ and p₂ can be gotten with:

e- is the element of our basis that squares to -1

What is P, geometrically? That’s the part I’ve prepared you for, the hyperbolic translation. It takes everything toward one of the points. P̃ takes everything toward the other.

What is v, geometrically? In CGA it will be a relatively random-looking sphere, with the nice feature that it is guaranteed to bisect the points. In the stereographic view it will be a hyperplane(/line) sitting between the two null planes(/lines). That’s all you need to know*.

What is Pv? The geometric product is transform composition, so it will be a reflection (v) followed by a movement (P). Here’s a simpler example of what we’ve got to think about:

Green reflction followed by red translation equals blue reflection. Note that the blue reflection is a moved copy of the green reflection; it has been moved by the red translation. Hmm, or wait a second, it has been moved by half the red translation. Weird, but you can get used to it.

So Pv will be a sphere reflection between the points followed by a push “all the way” to one of the points. A reflection in a sphere followed by a movement all the way towards a point inside that sphere will be, in some sense, a sphere reflection at that point. That is, a reflection in a sphere there. That sphere will have zero radius. And a zero radius sphere at a point is in some sense the point itself, QED.

The philosophical implications of extracting a point from a point pair

Listen to me: P is really weird.

1. There is no real number λ (“hyperbolic distance”) such that coshλ + Bsinhλ = P. But, it turns out you can reasonably argue that you would get something like P if you set λ = ∞. One way to say it is that ordinary hyperbolic translations will take you toward p₁ but not reach it; P, which we defined additively (usually a bad thing! You should define things multiplicatively!) lets you reach it.

2. You probably thought P̃ was the inverse of P; actually, PP̃ = 0, and neither of them have an inverse. This means they are part of no group - I used to think all the “useful” elements of a Clifford algebra were in a part of it called the Clifford-Lipschitz group; I no longer think that. Interestingly, in this sense, our ~ operation is more powerful than inversion.

3. PP = P. Geometrically that tells you that shrinking down onto the surface of a zero-radius sphere… and then doing that again… is the same thing is doing it once. Perhaps not so surprising - but still not like any transformation you encounter in your day to day life like rotations or translations. This is called being “idempotent”.

P goes by other names. “Projector” is what it’d be called in ordinary quantum physics; things called “Spinors”, rather mysterious objects, are defined in a way that is intimately bound up with projectors. P is also what Basil Hiley would call a “groupoid”. He originally read about them being studied by Clifford. He and others would say that space-time points (“events”) should be understood using them; this is an interpretation of the philosophical “process theory” of David Bohm, where there are no geometric objects, only transformations, with apparent geometric objects being limiting cases of transformations.

*Ok, a little on v. It’s a very basis-dependent object; in principle, e₋+e₁ or any other negative-square 1-vector would work just as well, but e₋ is easiest to write. Depending on what choice we make (and what its norm is), we can change the “magnitude”s and perhaps the orientations of our final p₁. The scare quotes because p₁, being a zero-radius sphere, is null - so it’s even less clear than usual what its magnitude means! Basis dependence in general is a sign that something is going to bite you one day. It’s not supposed to matter because any sphere v that isn’t incident with either point should give you the same p₁ up to magnitude and orientation. What a bizarre thing to have to do though! I think there are unanswered questions here.