Line-sphere intersection in Projective vs Conformal Geometric Algebra
Yes, you *can* use quantum physics and hyperbolic geometry, but are you sure you *want* to?
This post looks at the treatment of a very simple problem. But most things you can do in CGA and PGA end up shaking out rather like this, so think of it as standing in for a lot of problems.
The pictures:
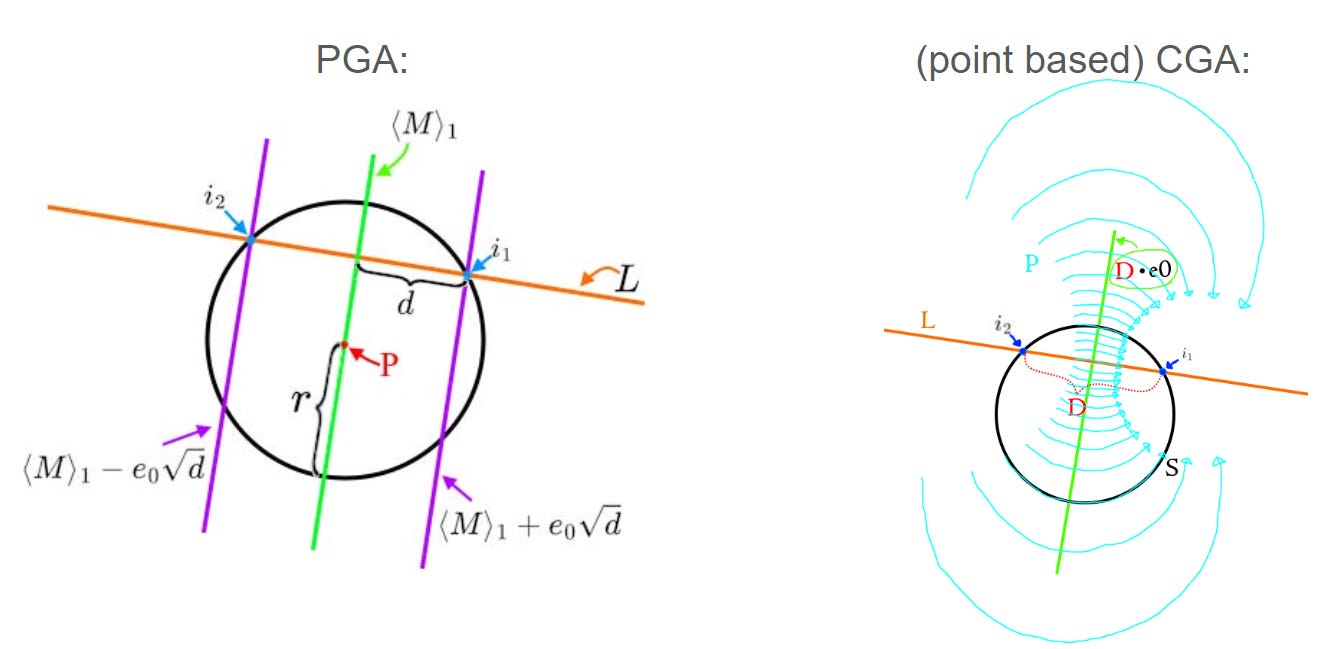
The algebra:
Both of these work in any number of dimensions.
I don’t usually use point-based CGA, but I’m ripping the “point pair extraction” method from Lasenby & Lasenby.
There is more uniting these two approaches than dividing them. Both involve a square root, and a projection of sorts, and both involve saying to yourself “oh yeah, I need e0” in the penultimate step.
PGA is faster but involves “stepping outside the algebra”, which maybe feels icky. On the other hand, it’s nice to represent spheres linearly - the coordinates of CGA spheres change nonlinearly with the position and radius of the sphere.
Another hidden disadvantage of the CGA approach is in the fact that probably, you will want the xyz coordinates of i₁ and i₂, and that will be a chore to extract from CGA (you will need to remind yourself of the existence of e0 again!). You get that for free from the PGA representation.
On the other hand, CGA has the advantage of, uh… making us feel cool because we’re using a concept from quantum physics? P is a “projector”! It is also a hyperbolic translation, like the horizontal hyperbolic translation you see here (thanks Eryk!):




