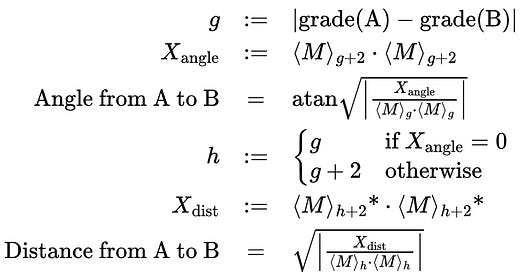Angle and distance from anything to anything, using Projective Geometric Algebra
So you want these:
And you would like them in a performant, general way. If this is your first time noticing the weirdness of the line-line case, be sure to spend a moment visualizing that!
How we’re going to do this (skip if you just want the formulae!)
Philosophically: angle and/or distance is a property of a transform from A toward B, which is their geometric product AB, call that M. M will have what we need “inside” it, albeit encoded in a way that we have to read out carefully.
So how do we extract angle or distance from M? We will look at ratios of how much M is like this or like that kind of transformation. For example, if M is a rotation (because A had 0 distance to B but had nonzero angle to B), it’s a case of checking how much like the identity M is and how much like a line reflection (180 turn, the “most drastic” rotation) M is. The “amount M is like the identity” is the magnitude of M’s scalar part, the “amount M is like a 180” is the magnitude of M’s bivector part. The ratios of these magnitudes gives us our answer!
But rotations are not the only transformations that have angle! Rotoreflections have angle, screw motions have angle! That’s ok though; instead of asking “how much like the identity (grade 0) is this rotation(grade 0+2)?” We’re asking “how much like a reflection (grade 1) is this rotoreflection (grade 1+3)?”. So we need to take the magnitudes of the correct grades of M. And fortunately, the kind of transformation M could have been can be deduced from what A and B were! We deal with this in the definition of an integer g.
One last thing we need to be aware of: sometimes A and B can be parallel. This implies that the transform taking A toward B is simpler than it could have been. Specifically, “where” (in the grades) you expected to find a rotation, you find a translation. Because the rotation “collapsed” to become the identity. We deal with this in the definition of an integer h.
Nine problems, one algorithm!
Alright then. For plane/line/point A and plane/line/point B, here’s how you get their angle and distance:
Additional detail:
grade(M) is 1 for planes, 2 for lines, 3 for points
⟨M⟩ₙ is the grade-n part of M
M* is the dual of M
As the C standard specifies, we need our atan funtion to give atan(1/0) = atan(∞) = 90 degrees. If that sounds weird, consider the angle of a right-angled triangle with opposite length a and adjacent length b, and let a go to infinity. I think this is cool! You can use atan2 instead of that makes more sense.
To walk though an example, say we want the angle or distance between a plane P and line L:
M = PL and g = |1-2| = 1
g+2 = 3 so X_angle is the squared magnitude of the trivector part of M.
Suppose P and L were at an angle of 35 degrees. Then M is a rotoreflection and the trivector part of M will be the point that it is a rotation around. X_angle will be sin²(35). The denominator in the angle formula will be cos²(35). Substitute those and you’ll see we get the right answer! Here, the plane part (grade 1) of M is bigger than its point part (grade 3) because M is more like a plane reflection than a point reflection (a rotoreflection with an angle of 0 is precisely a planar reflection, a rotoreflection with an angle of 180 degrees is precisely a point reflection).
Suppose P and L were parallel though! Then they have zero angle (so h=g), and we want their distance. Instead of being a rotoreflection, M will be a glide reflection. The grade 3 part of M will be a point at infinity, whose magnitude we get with the X_dist formula. It’s similar principles at work again to give us the distance!
Cheap version that sometimes breaks!
The above maybe seems over-engineered. Really, parallelism is “unlikely”, and when you’re measuring distances it’s usually distance to a points - and with points, X_angle is guaranteed to be 0! This allows you to ignore the parallelism “check” we encoded in the definition of h.
Arguably nicer because you get to visualize X∨P, the object whose norm is the distance, as a line/plane/thing with length/area/volume.
In the case of point-and- plane, you can even drop the norm and just use the scalar part - which will be negative or positive depending on which side of the plane the point is on! Personally I prefer thinking about that kind of thing this way, although I have to admit that the oriented-volume kind of object is useful for, eg, finding out whether a point lies inside an object.
The above also makes use of these, the norm, normalization and join: