A Clifford Algebra encompassing rotations, translations, uniform scalings, and camera FOV changes
An alternative to 4x4 matrices! Also includes a way to visualize Conformal Geometric Algebra
Game developers like 4x4 matrices because they can perform:
Rotations
Translations
Scalings
Perspective camera transforms
4x4 matrices can also do shear transforms, which absolutely nobody likes. Partly for that reason, game developers often switch to quaternions or dual quaternions, which can do rotations and translations without any risk of accidentally spilling over into a shear. Unfortunately, dual quaternions can’t do the desirable scaling or perspective-camera-stuff.
Or can they?? This writeup will present an algebra capable of both of those things, still without any risk of becoming a shearing. Here’s a bit of trippy fun to acquaint ourselves with a transformation which, in this algebra, is fundamental:
The Hollywood jargon for these is “dolly zooms” or “zollies”. The effect is achieved by moving the camera backwards while simultaneously zooming. The mathematical terms (I have found…) for them is “perspectivities” or “homographies”. But actually that is more general term: it includes rotations and translations. I want to talk about this transformation on its own - so, following Hollywood, I propose to use the term “zolly” for these continuous transformations. Zollies are a subset of perspectivities which preserves all the points on a particular plane. Or rather, that’s what they are in 3D. In 2D, instead of a plane they preserve points on a particular line.
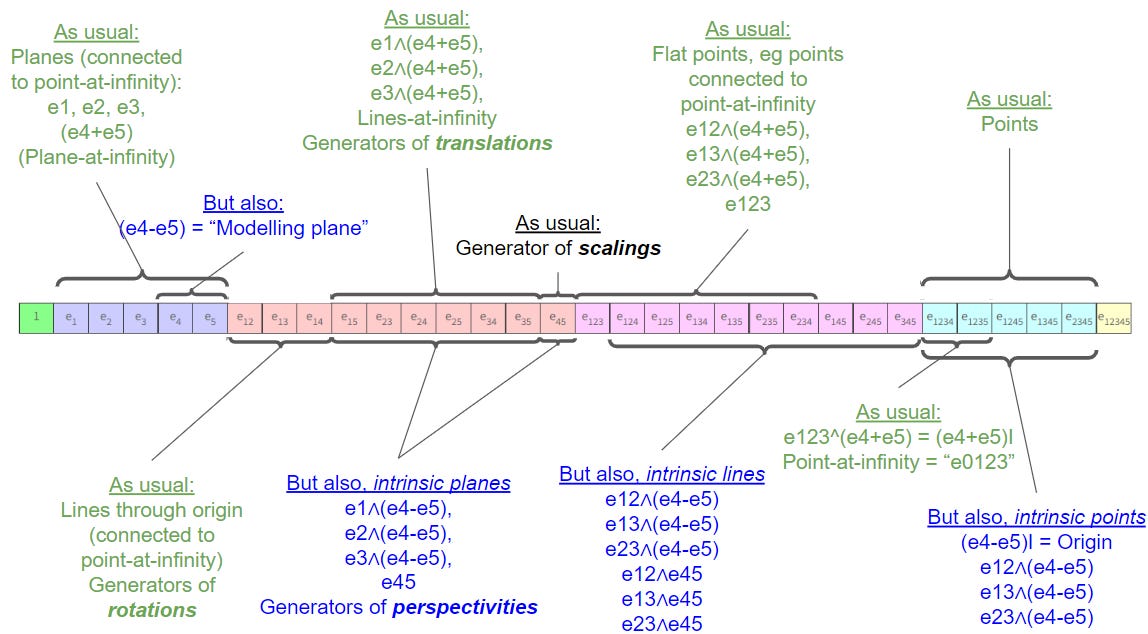
The picture below shows the 3D version of the algebra this writeup will be working towards - so, don’t expect to understand it just yet! It’s Cl(4,1) with a new geometric interpretation for half the elements. Green text indicates that the obects are included in plane-based Projective Geometric Algebra (PGA). Black is marginal; scalings aren’t in PGA but will be familiar to some people. Blue things are in Camera GA - but the only other place you might have seen them is in the work of Charles Gunn or Eric Lengyel:
For now, at least, I’m calling it 3D “Camera Geometric Algebra”. This deliberately overloads the existing acronym “CGA”, which usually means “Conformal Geometric Algebra”. Funny thing, though: Conformal GA and Camera GA are the same algebra with a different geometric interpretation! Later, I will focus directly on Conformal GA, and if you’re more interested conformal transformations than camera transformations then you can treat a large part of this document as an exposition of the embedding of plane-based PGA in Conformal GA!
In 2D, Camera GA is Cl(3,1). That’s much simpler, and everything generalizes quite predictably to 3D, so 2D will be looked at more than 3D.
Here’s how this writeup will progress:
Plane-based euclidean PGA review
Review of models of hyperbolic geometry. It will turn out that n-dimensional Camera GA is (algebraically) equivalent to (n+1)-dimensional hyperbolic Plane-based PGA!
Plane-based hyperbolic PGA, and hyperbolic motions
Comparison with Conformal Geometric Algebra - which is also algebraically equivalent to (n+1)-dimensional hyperbolic PGA! You’ll like this if you’re interested in conformal GA; if you’ve never done Conformal GA, you can skip this!
Point-based PGA review. Where previous parts test your geometric imagination, this will test your patience for notation and pedantry!
The main event: how 2D point-based PGA can be embedded along with plane-based PGA into Camera Geometric Algebra, Cl(3,1). This gets us the algebra with rotations, translations, uniform scaling, and zollies
1. A review of euclidean Plane-based PGA in 2D (which generalizes perfectly to 3D)
Really, this article is for people already very familiar with this system - unless you know the below very well, venture no further! We’ll be riffing on it in many different ways below.
2D PGA starts by saying that we have e₁, e₂, and the special e₀. e₁ and e₂ square to 1 and e₀ squares to 0. These are basis elements of Cl(2,0,1). But that’s just an algebraic description; you have connect the algebra with the geometry by labelling bits of geometry in a clever way that makes the algebra start solving problems. The one I’ve been using for multiple years now is the “Plane-based Euclidean PGA” (plane as in hyperplane, so the “planes” for 2D are lines):
PLEASE NOTE GOING FORWARD: That big circle there - it is not meant to be a circle! It is a circle-that-is-actually-a-line-at-infinity. It should be thought of as being somewhere on every diagram in this writeup, but you only see it on a few like this one. Here, e₁, e₂, and e₁₂ are where they should be. But, that circle, well actually it should be off the page, because it is actually infinitely far away from e₁₂ in every direction, because it is actually a circle of infinite radius - and a circle of infinite radius is actually a line. In plane-based PGA, this circle-that-is-actually-a-line-at-infinity gets labelled e₀ as you see here - but at other times it will go by other names. I’ve also marked e₀₁ and e₀₂ - they are the points where e₁ and e₂ cut e₀. But what I just said applies to them as well: e₀₁ and e₀₂ should be thought of as being infinitely far away from e₁₂.
Sometimes, people draw this picture of e₀:

So, e₀ is like the horizon in a landscape picture (in this case, a landscape containing a pair of railroad tracks that we are looking up, with some cactuses by the side, and the moon and stars in the sky). That’s a good way to think about this line-at-infinity, but the previous picture will serve better in general.
We can make any line in the plane by adding together the elements we have just defined:

A line, on its own, in plane-based 2D PGA, can perform a reflection, sending everything from one side of the line to the other. There are two other tools we define called the geometric product and the wedge product (Eric Lengyel calls what we are just about to define the anti-wedge product and anti-geometric product; we’ll get to this eventually!). Taking the geometric product of two lines in 2D gives you a transformation that is a reflection in one line followed by a reflection in the other; this will be, precisely, a rotation around the point where the two lines intersect. And the wedge product of those two lines will be that intersection point on its own. Some more examples:
e₁₂ = e₁∧e₂ is the intersection of the line e₁ and e₂, as shown on the diagrams
e₁ + 3*e₀ is a line parallel to e₁
0.96e₁ + 0.28*e₂ is a line very close to e₁, but angled slightly towards e₂. It can be used to reflect any element in it
0.96 + 0.28*e₁₂ = e₁*(0.96e₁ + 0.28*e₂), is a slight rotation around e₁₂
1 + 3*e₀₁ is a translation that preserves the point e₀₁, which is where e₀ and e₁ meet (their wedge)
e₁ + 3*e₀₁₂ is transflection
Euclidean transformations are the “even subalgebra” aka “spinors” aka “lie group” of this system, and the points (generally: the grade-2 elements) are the lie algebra. For example, exp(e₁₂*t), with exp defined by Cl(2,0,1)’s multiplication, will give a rotation around e₁₂ by an angle proportional to t.
One last thing about PGA. The wedge product “∧” is sometimes known in plane-based GAs as the “meet”, which makes sense in that context. There’s a related operation in PGA called the “join”, and it has been part of PGA since it was first described by Jon Selig in 2000. But for the purposes of this article, it’ll honestly be best if you pretend that you’ve never heard of the join being part of plane-based PGA. For some people, the join was always a source of concern, and was a reason to advocate other geometric algebras over plane-based PGA. We’ll get to this.
2. Hyperbolic geometry - my years spent reading about it were not in vain!
Plane-based PGA can be used to do non-euclidean geometry, including hyperbolic geometry. I previously viewed this as a “recreational” aspect of PGA, something that was amusing and maybe fundamental, but not relevant to my interests as a practitioner of computer graphics.
But hyperbolic geometry turns out to be the exact thing we need to create perspectivities! Specifically, it’ll turn out that they are what you get when you take a certain distorted model of hyperbolic geometry and literally look at it from the correct angle.

So, hyperbolic geometry:
This is the “Klein disk” picture of hyperbolic geometry. There are two other circular things you might mistake it for, and I am at pains to distinguish the Klein disk from them:
The boundary of the Klein disk is not the same thing as the circle-that-is-actually-a-line-at-infinity in the picture above. Ok, there is a vague analogy between them, which is that using each one’s definition of “distance”, both e₀, and the boundary of the Klein disk, are of infinite distance from the points inside them. But I’ll say no more than that about this particular connection. It’d be confusing to dwell on it, because we are going to be building a specific connection between the Klein disk and euclidean. But that’s a very different connection from this connection
The Klein disk is different from the Poincaré disk, which is the more common way of seeing hyperbolic geometry. Poincaré is more aesthetically pleasing, so you see it used more often. Here’s a comparison from this beautiful video:
The angles you measure on the Poincaré disk are the actual angles you would measure if you were in hyperbolic space, which is nice - but straight lines are bent into circular arcs. In the Klein disk, any straight line you see corresponds to an actual straight line you would see if you were in the hyperbolic space, but angles get squeezed a lot.
Choose your poison; both are distortions. Arguably, using the visual faculties we’ve evolved with, one will never really see 2D hyperbolic space (and later we’ll be thinking about 3D and 4D hyperbolic space, even worse!). And actually, this is ok, because we are not interested in hyperbolic geometry; we’re interested in solving problems in euclidean and camera-related geometry, which we’re going to do by exploiting aspects of the Klein disk model of hyperbolic geometry.
There’s another picture of hyperbolic space worth mentioning. It is called the hyperboloid model; below is a diagram of it along with the Klein disk picture, which I modified from one I found on stackexchange:
The hyperboloid extends infinitely far upwards, becoming tangent to a cone with its tip at the the eye. With the eye at that tip, looking up the axis of the cone, the hyperboloid looks exactly like the Klein disk. The hyperboloid appears like a circle, because cones are circular.
Things to know about the hyperboloid model:
Like the Poincaré and Klein disk, this hyperboloid is a distortion of hyperbolic space. Knowing a euclidean distance between two points on it would not tell you anything about their actual relationship to one another, any more than their distance on the flat Klein disk would.
The hyperboloid picture of 2D hyperbolic space requires you to visualize a 3D ambient space - and that won’t last you long, because we will shortly be thinking about the Klein 3-ball, which would have this same relationship to a hyperboloid sitting in 4D space! Nobody can visualize 4D space; don’t believe anyone who tells you otherwise. To help us manage the maths of it, all we have are tricks!
Since it’s so rubbish, why did I bring the hyperboloid model up? Partly because:
“Point on the disk” <=> “Ray in the ambient space, coming from the origin”
Is a particularly useful trick. It’s called the Klein view.
Another thing: I used to think only points inside the disk were “valid” in some sense. Now I know better, because you can have any ray you like:
Points can be inside the disk (their ray pierces the hyperboloid)
Or outside the disk (ray does not touch the hyperboloid)
Or on the boundary of the disk (ray is tangent to the hyperboloid, at infinity)
Euclidean and non-euclidean motions
In hyperbolic geometry, rotations and angles are a thing, but translations and “distances” work differently. The general term going across euclidean and non-euclidean geometry is a “motion”. Let’s define these motions for 2D geometry.
A euclidean motion could take some angle and rotate by it; or it could take some distance and move by it. This is so boring I won’t include a visualization!
An elliptic motion could take some angle and rotate by it, or it could take… some other angle and rotate by it. There’s an animation of 2D elliptic space from Zenorogue below. It’s just what you would see if your eye was at the center of a globe - that’s all 2D elliptic space is, a globe:
Hyperbolic motions are a zoo from which we shall recruit several illustrious animals! As with euclidean and elliptic, you can take some angle and rotate by it around the center. But at another extreme, you could take some “hyperbolic angle” and… well, take a look at this klein disk performing a rotation followed by a hyperbolic translation:
Again from Zenorogue, this is what hyperbolic motions can look like, visualized with the Klein disk. Where ordinary elliptic rotations are handled with cos and sin, a hyperbolic translation is accomplished with cosh and sinh (also: mathematically, hyperbolic motions are equivalent to lorentz transformations).
3. Using hyperbolic PGA to explore the zoo of hyperbolic motions
Remember the circle-that-is-actually-a-line-at-infinity? Hyperbolic space has one of those as well: it is much bigger than the Klein disk, and surrounds it. In order to get a model of euclidean geometry, we gave the label “e₀” to the circle-that-is-actually-a-line-at-infinity, and we asserted that it squares to 0. But the one for hyperbolic space gets the label e₋, and we assert that it squares to -1.
All of 2D plane-based hyperbolic PGA drops out of that one replacement of a 0 with a -1! Including all the crap above! Here’s a picture comparing 2D euclidean plane-based PGA with 2D hyperbolic plane-based PGA. e₀ and e₋ are left out of them - because they are infinitely big circles, far off the page!
Everything looks the same - the way coordinates work has not changed aside from relabelling e₀ as e₋. Also the same is e₁ and e₂, which perform ordinary-looking reflections in lines that pass through the origin. Consequently, e₁₂ and any rotation generated by it will also perform rotations around the origin. But everything else is slightly, or completely, different:
A semi-familiar case is a rotation preserving a point that’s just inside the disk, such as e₁₂ - 0.5*e₂₋. This will do a rotation-ish thing; everything will go all the way around it as usual, but things will get bunched up, accordion-like, along the way, in order to stay inside the disk
How about a rotation around a point just outside the disk, such as e₁₂ - e₂₋ - e₁₋ ? These guys are very weird, having a scissor-like lorentz-like motion. The bottom-right point is like this: it’ll move stuff around it alright, but look at the lines that cross where it is - if you’re in a quadrant made by those two lines, your motion won’t move you outside it
One can also “rotate” around a point (not pictured, because again I can’t!) sitting on e₋, infinitely far outside the disk. A transformation generated by such a point will send things directly across the disk. The horizontal-fisheye movement in the Zenorogue gif above is an example of this.
A reflection in a line (so long as the line is partly inside the disk…) looks kinda like an ordinary reflection, but it doesn’t take things as far; it’s a hyperbolic reflection rather than a euclidean one
But the most important case is rotations around points on the boundary. These matter so much that I might as well say the technical term for them, which is parabolic rotation. Elements that generate parabolic rotations always square to 0 - in fact anything, for example a line, that is tangent to a Klein disk, squares to 0.
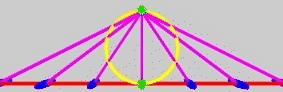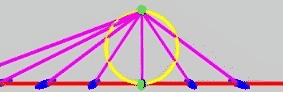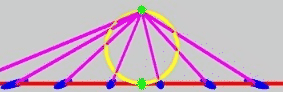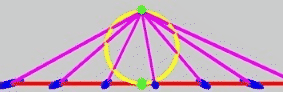
I’ve made two animations of parabolic rotations for you, with caveats to come after. Here’s one parabolic rotation of some magenta lines:
Hmm, what’s that happening to those blue points on the red line? Could it be… yes! It’s the first appearance of a zolly! It’s in 1D, which is incredibly useless - I mean, what would it even mean to have a camera in 1D, let alone a camera transformation? But from small, green acorns do mighty algebras grow! Correction to this gif, by the way: I should have made the green point on the north pole rotate around the circle in this one, sorry.
This is an animation by Roice Nelson of a parabolic motion. I include it because it is beautiful, but alas it is also an irrelevant animation because it is in yet another different model of hyperbolic geometry that I am not using called the upper-half-space.
A Klein view of 2D euclidean geometry inside the Klein model of 3D hyperbolic geometry
Again at heart I’m a game developer - in general I like my ice cream vanilla, and my geometry euclidean! Well, it turns out that you can do euclidean geometry using parabolic motions in the Klein disk. Take a look at this parabolic motion of those same magenta lines:
In this one, the blue points are experiencing a euclidean translation along the line. I can safely say this is the worst case of programming a sledgehammer to crack a nut that I have ever been guilty of: a euclidean translation in 1D can be modelled by… just… adding… a number… to other numbers… argh!
There again, it’s interesting that it’s implemented by the same sort of thing as a zolly, wouldn’t you say! Caveat: the bottom green point, and the red line, should move - and the blue points, marking where the red line meets the magenta lines, should of course move with it. It’s ok though! I think 🤷
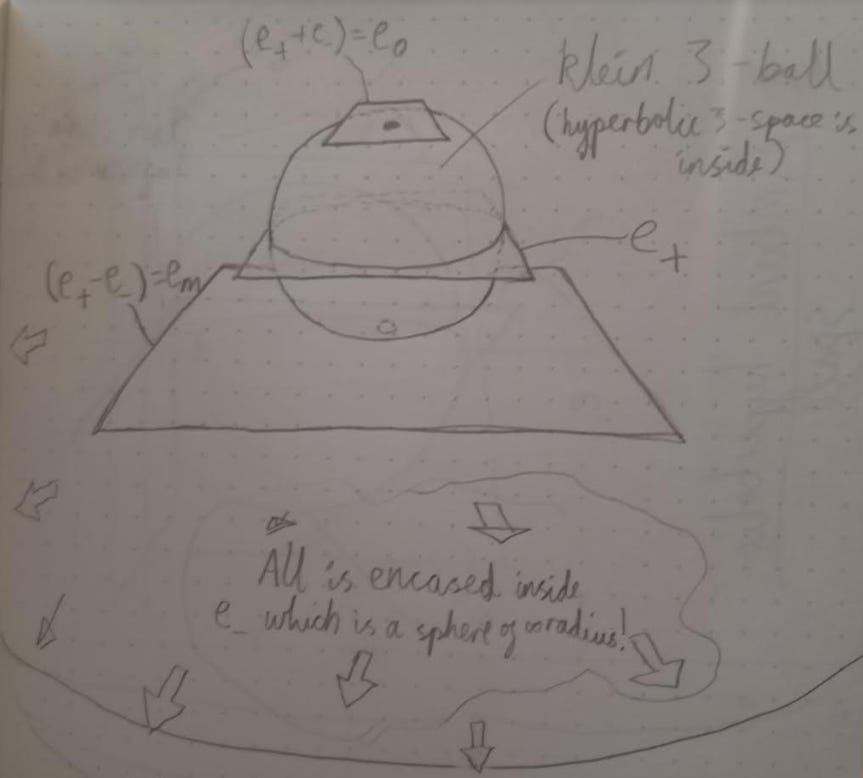
Alright, we have euclidean motions and zollies in 1D geometry, but 1D geometry is so boring that you have to be a pedantic mathematician to even call it “geometry”. So let’s be a bit more exciting with some 2D geometry - but in order to do that, we have to step up a dimension and think about the Klein 3-ball - that’s just the 3D version of the klein disk, no biggie. Here’s some planes in a Klein 3-ball, performing some rotations and hyperbolic translations:
We modelled hyperbolic geometry in the Klein disk using Cl(2,1), 2D hyperbolic PGA. We can model the Klein 3-ball with 3D hyperbolic PGA Cl(3,1), i.e. an algebra generated by three elements that square to 1 (three orthogonal planes passing through the center) and one element that squares to -1 (the “sphere-that-is-actually-a-plane-at-infinity - it’s the black background of the gif above).
What will we call our basis planes? From 2D hyperbolic PGA, we’ll keep the labels e₁ and e₂ for two of those planes through the center (the “x” and “y” planes if it pleases you!), and e₋ for the sphere-that-is-actually-a-plane-at-infinity. The other plane we’ll call e₊, since it squares to +1.
Wait, what? Why it e₊ instead of e₃, seeing as e₁ and e₂ square to 1 and so does e₊? Well, if hyperbolic PGA was all that we wanted, then sure, that’s what I’d call it. But we’re about to do something important that treats e₊ very differently from e₁ and e₂. You see, there are two planes parallel to e₊ that are vitally important. Here’s a picture:
The eₘ plane will be important later. We’ve labelled the plane tangent to the north pole e₀ because, combined with e₁ and e₂ and a certain choice of viewpoint, we can construct… 2D euclidean plane-based PGA!:
Again we’re using the Klein view: you put your eye at the marked point at the north pole and, from your point of view…
Most lines through that point/your eye look like points
Most planes through that point/your eye look like lines
The unique plane through your eye perpendicular to your view direction might look like a line, except that it’s a line you couldn’t possibly see it. Think about this until you see why it is labelled e₀!
Lines through your eye that lie in e₀ might look like points, except that again you can’t possibly see them while looking forwards. So, these lines, such as the line marked e₀₁, where e₀ meets e₁, are our points at infinity!
These geometric elements, all passing through one specific point (technical term: “in the point’s bundle”), form a subalgebra of that geometric algebra. And because the point we have chosen sits where it does, this particular subalgebra of Cl(3,1) is… Cl(2,0,1)! Euclidean plane-based PGA!
The very coolest thing is that the point where your eye sits is the pseudoscalar, e₀₁₂. I’ve sort of written about this before; to my knowledge, this is the best visualization of the PGA pseudoscalar one can manage!
4. A digression on the other CGA, Conformal geometric algebra

This section is only for people familiar with Conformal GA. If that’s you, you will already have recognized part of what I’m constructing. A model for 2D euclidean space, using Conformal GA, has the signature Cl(3,1), just like Camera GA, and Conformal GA, you’ll mark e₊ + e₋ as being special, which is what we have done above.
Usually, Conformal GA is point-based - and indeed point-based Conformal GA will resemble our final result. But so far we’ve been plane-based, eg e₁ and e₂ are orthogonal lines through the origin (or rather, they appear to be lines-in the ambient space they are planes!).
Some people, like Steven De Keninck, do advocate sphere-based CGA. e₊ would be the unit circle around the origin (this will be the first and last time you will get a single object representing an actual circle in this article!), and e₁ and e₂ are planes as usual. It works because a plane is “just” a very large sphere. In that view, what we have so far is - precisely - the plane-based-euclidean-PGA subalgebra of sphere-based CGA.
But that’s not where I’m going. A key difference is that in Conformal GA, points are generally meant to square to 0 (otherwise, they are “imaginary” points, which you can’t see). When I want to do 2D Conformal GA (which I sometimes do!), I keep two pictures in my head, again one 3D “ambient” and one 2D “Klein view”:
This is extremely similar to the above (it is a superset of it!), but you have more stuff. I’ll be adding more stuff too, but it’s going to be subtly different stuff.
The thing to know is that in Conformal GA you only see something in the place that it meets the surface of the Klein ball:
e₊ is a plane in the ambient space, but it looks like a circle - because when you cut a sphere with a plane you get a circle. Oh dear, I’ve drawn yet another origin-centered circle that I have to say is subtly different from the others in terms of the algebra! Well, it is. Sorry.
e₁ and e₂ look like lines because each one of them is also a place the sphere has been cut by a plane, but the circles created on this occasion pass through your eye - and if your eye is pierced by a ring (do not google this…), the ring will look like a line
p₁ and p₂ are points lying on the sphere in the ambient space, so you do get to see them as exactly what they are - points
p₃ is a point in the ambient space - but it isn’t on the sphere, so you don’t see it!
e₊₁, e₊₂, and PP1 are each lines in the ambient space, but they each pierce the sphere in two places, so you see them as what are called “point pairs”. These things are connected, but not in a way you can see (because you can’t see the interior of the sphere, only its surface). A point pair (PP) is a single geometric object; they are a necessary part of Conformal GA, and they are quite interesting because in 2D they generate spinors (handedness-preserving conformal transformations).
PP2 is a line in the ambient space - but again it isn’t anywhere near the sphere, so you don’t see it
PP3 is a line tangent to the sphere in the ambient space. You see it as… a point?? Weird! But really it is still a point pair, just a point pair where both points are in the same place (yes, this is getting a bit insane)
PP4 and e₁₂ are interesting. They are, again, lines in the ambient space, so a priori you’d expect them to be point pairs. And indeed you do see one point of theirs, but the other point is precisely the point where your eye is. And you can’t see your own eye, so you only get to see one point in the point pair.
One more thing, which in the ambient space is a line, is (e₊+e₋)e₂. This line is tangent to the north pole, so it combines the conditions that apply to PP3 and to PP4 - you might say it is a point pair where both points are the point at infinity (someone please stop this madness). If you were doing Camera GA, you could say it is a line connecting the point at infinity with a point that is far off in the distance of the ambient space, perhaps e₊₋₂!
This ludicrous proliferation of cases for “point pairs”, which mostly consists of things that can’t be visualized as pairs of points(!), is part of why I’m sceptical of Conformal GA going mainstream, at least not in the era of Tiktok. That being said, you might have noticed the analogy with the Riemann sphere, and indeed this is precisely how you can visualize mobius transformations within a geometric algebra.
There is already a paper on PGA as a subalgebra of Conformal GA, but with this setup we can say the connection between the two of them in a way that is very geometrical (and plane-based):
A bundle of geometric objects in Conformal GA, Cl(n+1,1), that pass through a single null point (your eye) in the hyperbolic space, will constitute a subalgebra isomorphic to PGA, Cl(n,0,1). These will be all elements that in any sense “include the point at infinity as part of themselves”, so:
All straight lines (circles that have become so big that they touch the point at infinity)
If you’re in 3D, all flat planes (spheres that have become so big that they touch etc)
The point at infinity itself (PGA’s pseudoscalar - I wish someone had told me it was n∞)
All point pairs where one or both of the points is at infinity
Here’s an excerpt from the first schematic of Camera Geometric Algebra I showed, showing how plane-based PGA sits inside it.
This is for 3D rather than 2D, so it’s Cl(3,0,1) inside Cl(4,1). Plane-based PGA sits in the algebra of plane-based Conformal GA in exactly the same way as it sits in the algebra of Camera GA. The difference is what I’m about to get to!
5. Point-based PGA
UPDATE: I have made a game illustrating this section! you can play it here. It is very difficult and it looks like this:
We’re well on our way to generating zollies, but first we need to discuss what has been called point-based PGA. Charles Gunn showed in his PhD thesis that point-based PGA is a model of a strange kind of space that Klein described as “Dual Euclidean” alongside the better-known hyperbolic, elliptic, and euclidean. In euclidean spaces, you can do translations; in hyperbolic spaces you can do hyperbolic motions; and it turns out that in dual euclidean space you can do zollies!

Independently of Gunn, Eric Lengyel also discovered the point-based-PGA/dual-euclidean-space connection. Eric succeeded in creating a single system that does both zollies and euclidean transformation - which is exactly what we want to do. Now that I understand it better, I think Eric’s system has been underappreciated. But going forward I expect to find myself using Camera GA, because it has only one product (the geometric product), whereas his algebra has two (the point-based PGA geometric product, which he calls geometric product, and the plane-based PGA geometric product, which he calls the anti-geometric product).
Apart from the labels we’ll get to, this system has the same coordinates as plane-based PGA, so addition works the same way (helpful for getting midpoints and bisectors!).
But the wedge product, in point-based PGA, does a different (though equally useful!) thing than it does in plane-based. If you take the wedge product of two points, you get the line that connects them - for example, taking the wedge of two points at infinity, you’ll get a line at infinity. Then if you’re in 3D, you can take the wedge product of a line and a point to get the plane containing them (previously the wedge did the “meet”). Now you know why Eric Lengyel calls plane-based PGA’s wedge product the “anti-wedge”; he reserves the term “wedge product” for point-based PGA’s wedge product!
This allows us to create pictures that have a geometric interpretation that is a lot more like some of the things people say in mathematics outside of GA. Directed lines, made by joining the origin with a point, look a lot like the things people usually call “vectors”, and if you wedge such a line with another point you get a clockwise-or-anticlockwise-oriented plane segment, which is what non-GA people often say a “bivector” should look like (if they mention bivectors at all):

Definitionally, the wedge product is always meant to be a part of the geometric product (or perhaps “anti-product”!). So, since point-based’s wedge product is different from plane-based’s wedge product, we should expect their geometric products to do different things too - and indeed they do. In 2D point-based PGA, the origin point squares to 0, and all other points (including points at infinity) square to a positive number. Most lines will square to a nonzero number; the exception is any line that has the origin sitting in it. These lines square to 0, just like the origin. It used to be that the line-at-infinity was a special line, and that specialness infected any points that lay on it. But now the line-at-infinity isn’t special; instead the origin point is special, and its specialness infects any lines that pass through it.
It’s time to say some notation for point-based PGA. Gunn and Lengyel have different systems for it; we’ll use Gunn’s. There’s another reason I’ve been delaying this part, which is that it can be quite hard to see the difference between point-based and plane-based PGA, once you see these labels, no matter whose notation you use!
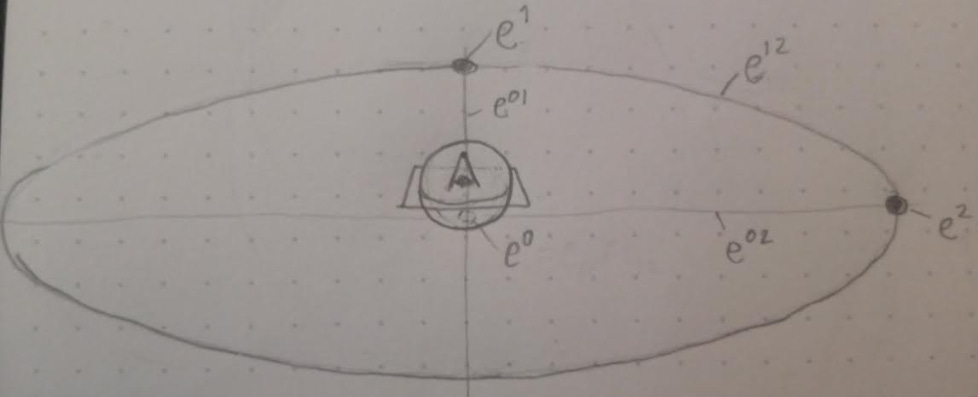
You write points as x*e1 + y*e2 + w*e0, and then lines are x*e01 + y*e02 + d*e12. Note the numbers are not subscripted - this is to distinguish them from plane-based PGA elements like e₁. If you don’t like this, don’t worry too much, because we won’t stay with it long! The whole point of Camera GA is to give a different way to do it!
Below is a picture. I’ve used superscripts for the numbers (which I can’t do on substack because formatting is weird for e⁰¹! Hence e01). It also has our old friend, the circle-that-is-actually-a-line-at-infinity. This time, that thing is e12 instead of e₀:
Looks pretty familiar, right? It’s just like the 2D plane-based PGA setup from earlier.
But in point-based PGA things are subtly different, in a way you can’t see. The headache-inducing thing you’re supposed to say to yourself when looking at, say, “e₁₂” and “e12” written nearby on a page, goes something like this:
“One of these is a point, one is a line”
“One lives in point-based-system and one lives in a plane-based-system”
“Both of these systems have coordinates that -apart from their labels- work in similar ways”
“The labels systems are related by a duality operation”
“But these different systems are in some sense different worlds! I mustn’t draw them overlapping in the same diagram, because if you want to transport something from one world to the other you have to use that duality operation, which is defined algebraically rather than geometrically!”
To make matters worse, if you want to go up from 2D PGA to 3D PGA, the first of those bullet points becomes a half-truth - you have to get planes involved, and lines change their nature.
Eric has a different notation that arguably avoids some of this confusion. He uses a single algebra which treats, say, e₁₂ as a single object (no need for it to be distinguished from some kind of “e12”); problem is, it’s a single object with two geometric interpretations, one in each system. In terms of leading up to an algebra containing euclidean transformations and zollies, there’s a problem with this: so far as I can tell, in his system, an object can have either a translation or a zolly applied to it - you can’t do one, and then the other, to a single thing. And that’s exactly what we want to do in Camera GA.
What I always wanted was a geometric interpretation of the relationship between plane-based PGA and point-based PGA - I wanted to draw them overlapping, in the same diagram! Anthony and Joan Lasenby advocate using elliptic projective GA for many problems, partly because you get something like that: multiplication by the pseudoscalar implements what’s sometimes called Poincaré duality. But elliptic projective GA sacrifices euclidean translations! And most of us really need those!
I think my approach of embedding both of them in Cl(n+1,1) solves this problem. So let’s see that!
6. The embedding of 2D point-based PGA into 3D hyperbolic PGA, aka 2D Camera Geometric Algebra
So here we go! The thing marked e12 is again a circle-that-is-actually-a-line-at-infinity. The sphere at the center is the Klein 3-ball and is sitting on top of the disk, with the disk’s center, the point marked e0, being precisely its south pole:
The plane tangent to the south pole of the sphere is what I call eₘ; m is for “modelling space”, because when we think about 2D geometry we’ll be, in a sense, doing it inside that plane. eₘ = (e₊ - e₋), and eₘ*eₘ = 0. I said above that in conformal GA, you only see something in the place that it meets the surface of the Klein ball. Well, in Camera GA, you only see something in the place that it meets the eₘ plane! Apart from that, Conformal GA = Camera GA.
Here’s the rosetta stone for plane-based-hyperbolic-PGA (whose elements are still written with subscripts) to point-based-PGA:
e1 and e2 (grade 1), points at infinity, have become e₊₋₂ and e₊₋₁ (grade 3)
e0 (grade 1), the point at the “origin” (not the origin of the ambient space, mind you, just the origin as you see it) has become eₘ₁₂ = e₁₂*(e₊ - e₋) (grade 3)
e01 and e02, lines passing through the origin, have become eₘ₁ and eₘ₂ (grade 2)
e12, the line at infinity, has become e₊₋, because e₊₋ = eₘ ∧ e₋ = eₘ ∧ e₊ (grade 2)
That tells you the coordinates and the wedge product. How about the geometric product of point-based PGA? To say this we will bring in Cl(3,1)’s pseudoscalar, I = e₊₋₁₂. Here’s how it works:
Point-based PGA geometric product of a and b := (a*I) * (b*I)
Where * indicates (what else?) the geometric product of Cl(3,1).
The join - in both Camera GA and Conformal GA - can be defined as ((a*I)∧(b*I))*I. That product always seemed so beautiful and simple to me - but I guess it wasn’t simple enough! The join, then, is a particular grade from my product above which you then dualize. Swap out the ∧ for another * to get Eric Lengyel’s anti-geometric product. There’s something Leo Dorst has been calling the “dual join”; this would be a subset of the product I’ve just described.
Bringing it all together!
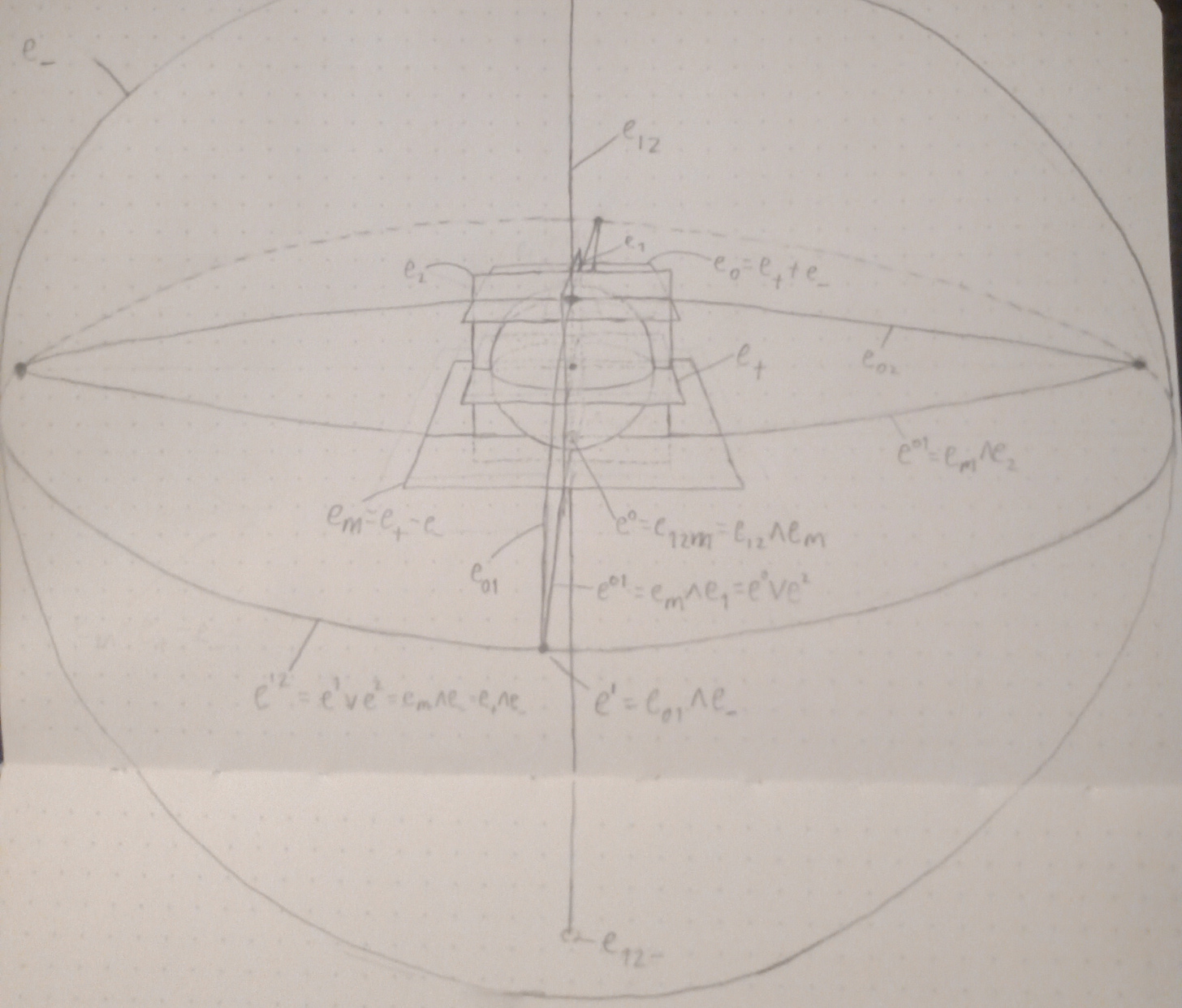
Here’s a picture of the embedding of 2D plane-based AND 2D point-based PGA in 3D plane-based hyperbolic PGA:
Here, the big sphere, e₋, is again a sphere-that-is-actually-a-plane-at-infinity. Those lines that meet each other in points on its surface are actually parallel, “meeting” each other infinitely far away from the center.
Across all geometric algebras, elements that are of grade 2 can be exponentiated. So zollies are exponentials of certain lines in this picture. Specifically, they are exponentials of the exact lines that they should be: lines passing through the south pole of the sphere, for example eₘ₁ and eₘ₂. e₊₋ exponentiates to a uniform scaling, aka “scalor”, aka “pure zoom” - and if you know your Conformal GA, possibly you already expected that part. Together, eₘ₁, eₘ₂, and e₊₋ form a basis for lines lying in the eₘ₁ plane. So, arbitrary lines in there such as (eₘ₁+e₊₋) exponentiate to a camera transformation with some amount of zoom.
Here’s the annotated algebra picture again, for 3D (with e₊ and e₋ written as e₄ and e₅, sorry!):
In 3D, the “zolly algebra” is isomorphic to the dual quaternions. Wait, what? I thought dual quaternions did euclidean motions? Yes, they do, but they also do zollies. If you want to do both, you need an algebra that contains two copies of the dual quaternions, overlapping at the quaternions. Cl(4,1) fits that bill!
And which kind of plane would you prefer, sir?
For every piece of geometry representable in GA, there exists a transformation or class of transformations such that that piece of geometry is invariant under that transformation, the canonical example being a straight line in space, which is preserved by rotations around that line (it this defines an “axis”). Therefore, when you see a plane, there should be an answer to this question: what transformation will it be associated with?
If you were only doing 3D plane-based PGA, you could be sure it was a reflection plane, i.e. a grade-1 object and it squares to a positive number (unless it is at infinity, in which case it squares to 0).
If you’re doing Camera GA, there is a new kind of plane. Its grade is 2, so you can exponentiate it to get a class of transformations. If it passes through the origin, it’ll square to 0 and exponentiate to a pure zolly; if it doesn’t pass through the origin, it’ll square to a positive number and exponentiate to a zolly-and-scaling (or just a scaling if it is the plane at infinity).
This applies for any geometric object you can see, which in 3D means points, lines, and planes. All of these now have two possible versions: a line could be grade 2 or grade 3, and a point could be grade 3 or grade 4. The grade-2 line is (as usual in plane-based PGA) a generator of rotation/translation. Everything else is just combinations of the above. Following Leo Dorst, I’m going to call these “intrinsic” versus “extrinsic” versions of the objects. Extrinsic is lower-grade, intrinsic is higher-grade, so for example an extrinsic plane (used for planar reflections) is grade 1, and an intrinsic plane (used for generating zollies) is grade 2.
It is extremely easy to convert between an intrinsic and extrinsic object. Here’s an illustration:
In this picture, both L and p would be seen by the eye as a point. L, grade 2, would be seen as an extrinsic point, and p would be intrinsic. Note that without “access” to e₀₁₂ you are “stuck in the (hyper) plane in front of the eye”, and without access to eₘ you are “stuck in the bundle of objects that pass through the eye”.
You can also add elements in the bundle to elements in the plane to get a combination of the two; the figure below shows this. These are perfectly practical objects, because an arbitrary camera transformation could have a rotation part and a translation part and a zolly part and a scaling part.

The picture shows the visual interpretation of these objects in the ambient hyperbolic space, but if you were doing 3D Camera GA, that space would be 4D - so what’s their visual interpretation given that our brains can do 3D at most? Well, for grade-4 objects we’re screwed - such things will have a geometric interpretation if, and only if, their e₁₂ₘ part is equal to 1. Although we have a crutch for the other objects: they will always have some intersection with eₘ, perhaps only at infinity. It’s far from ideal, because it means that you could look at an object and if it not entirely contained in eₘ, it really could be sticking out any old way in 4D. But at least it’s some geometric interpretation - and that’s more than you get in Conformal GA!

7. A random assortment of closing thoughts
This algebra might be a headache, or it might be great! The question I’d love to know the answer to next is if this system can be usefully used to visualize what get called covectors in the rest of linear algebra. It’s been said that linear forces are covectors; possibly this is the right way to embed that in one big, visualizable, system.
A common operation in computer graphics is to make a triangle’s plane from three points. Usually this is done by getting the normal vector by taking the cross product of the two edge vectors. Using the join found in this system, the triangle would be a zolly-generator. I don’t know if that’s useful for anything!
Same as Conformal GA, we have the very nice and useful property that if you want the distance between the origin and an object, you just take that object’s inner product with itself. At least, that works for intrinsic objects! If it’s extrinsic, just convert it to an intrinsic object with the eₘ∧object trick above. A potential geometric interpretation of this is that a plane at the origin is a pure zolly and a plane at infinity is a pure scaling, so the plane’s distance from the origin is seen in “how much of a scaling it is”.
A nice generalization of the above though is: if you have some two intrinsic points, and you take their join, you’ll get a line whose magnitude is proportional to the points’ distance. Take the join of three points enclosing a triangular area, and now you have a plane whose magnitude is proportional to that area. Four points, you get a copy of eₘ, and its magnitude is proportional to the volume of the enclosed tetrahedron. I don’t know how to generalize the geometric intuition here!
One problem of PGA is that some objects have norm 0, either in plane-based when they are embedded in e₀, or in point based when they pass through the origin. On the face of it makes it so that you can’t figure out “how much they have been scaled by”. Lengyel solves this with the “bulk” and “weight” norms, which are at least superficially similar to Gunn’s “euclidean” and “infinity” norms. Camera GA has a different solution: for any object-at-infinity, you can take its inner product with object with e₋ and taking the norm of that in the usual way. Or, join with e₊₁₂. The latter can help construct something more like the Poincare dual, so might be more fundamental.
What Charles Gunn calls the “infinity norm”, and what Eric Lengyel
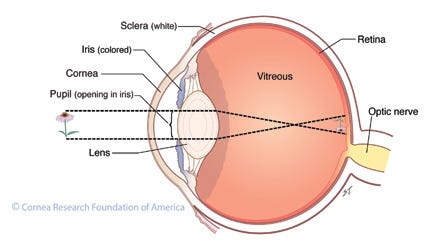
There is a distinct feeling to me that this setup - or something like it - has some connection with the anatomy of the eye:
In the above, when writing subscripts, I have been ignoring signs. For example, eₘ₁ should possibly be eₘ₁. I may well even have forgotten a factor of 2 in places; possibly eₘ and e₀ should be defined as half of what I defined them as, or even with a factor of 1/sqrt(2). That said, apart from when you exponentiate or add, these factors really ought not to matter.
The wikipedia article about homographies tells us something we see in the conformal section: that there is a known connection between perspectivities and conformal transformations. The nice thing about what I’ve described here is that it’s all a visualizable coordinate system, which I’m not aware of existing before. Relatedly, Conformal GA has a connection to AdS/CFT (CFT is the conformal part, hyperbolic PGA/“Spacetime Algebra” is the AdS part). I wonder whether this could offer at least some visual insight into that.
To say it one more time: in Conformal, everything that can be seen is as the place where it intersects a (hyper-)sphere. In Camera, everything is seen as the place where it intersects a (hyper-)plane. So we should ask - what if you do that with a hyperboloid? Well, I’m pretty sure you get the Poincaré model of hyperbolic geometry:
Acknowledgements
This research was conducted at Imagination Technologies, who took a chance on some weird maths! Huge thanks for productive discussions, teaching and feedback to Chris Doran, Leo Dorst, Charles Gunn, Steven De Keninck, Joan Lasenby, and Eric Lengyel.