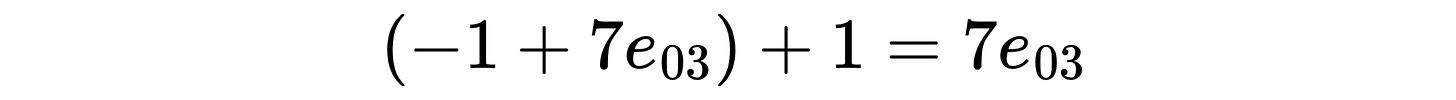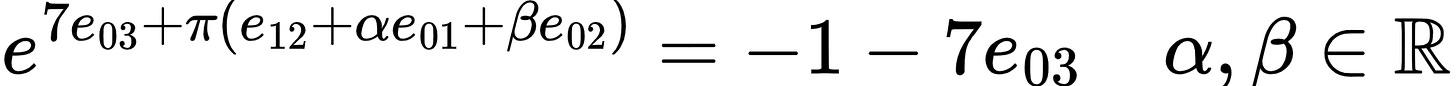360-translations - the strangest objects in Projective Geometric Algebra
Advanced Projective Geometric Algebra! Also, the Principle of Stationary Action
Reminder: the (ordinary) quaternions have a property called the double cover. For every “orientation” you could get to, there are two quaternions, with one of them taking you clockwise, the other counter-clockwise.
The double-cover property is very useful for computer graphics! If you have an animated character who wants to pick up an apple, you want them to turn their hand the correct way; matrices and vectors don’t distinguish clockwise/counter-clockwise, so they’re crap for animation compared with quaternions, because quaternions do distinguish. Here’s an intro if this is news to you.
Further reminder: Dual Quaternions are a part of PGA; they are very useful for animation; they can represent rotation and translation. We like dual quaternions. They interpolate better and they are more readable than matrices - the axis of a rotation will be represented as 6 floats within the dual quat (as plucker coordinates).
Like quaternions, dual quats have the double cover property when they’re used to represent rigid transformations. All rigid transformations.
This leads to a strange, horrible, but maybe-beautiful question: I know what “clockwise” and “counter clockwise” means for a rotation, but what does it mean for a translation?
A semi-likely situation in which you encounter unlikely objects
Reminder: in GA, to get the transformation that takes you from one object A to another object B, you take √(BÃ). If you were an innocent newcomer like me, you might misremember the formula as just BA, which is slightly different.
You have some transforms A and B. You’re thinking about transform A followed by transform B - that’s their geometric product BA. A and B could be rotations, translations, planar reflections (planes), screws, etc.
A and B could well also be points - that is, the transforms they encode are point reflections. What’s the geometric product of two point reflections? Here’s an example:
That result is a translation - of a sort. But it is a metaphysically bizarre translation!
Let’s briefly fool ourselves that we understand the situation. Here’s a factorization of the above (check!):
e₁₂e₃ is a 180 rotation (e₁₂) and a planar reflection in a plane that is orthogonal to the 180 rotation axis (e₃), which gives the point reflection e₁₂₃. (e₃+7e₀) is also a plane orthogonal to e₁₂. So the complete pile of transformations involves two 180 rotations around the line e₁₂ and two reflections in a pair of planes that are parallel to one another and orthogonal to e₁₂. In total, that’s a translation and a 360 degree rotation. This isn’t so surprising, since 1+7e₀₃ is a translation and -1 is a 360 degree rotation. Multiply (compose!) those to get -1-7e₀₃. Drawing this previous paragraph is an exercise the reader should be capable of!
So, it’s just the composition of two things you recognize - seems like no biggie! Also we see a reasonable name for them: 360-translations, that is, a negative scalar added to a null bivector. Different names have been suggested, including “Looped translations”, “cursed translations” and “nega translations” - because they’re negative in some sense.
There is more to these objects than meets the eye. 360 translations is good, but in this article I’ll go with “nega translation” because that evokes the Sailor Moon/Darkwing Duck negaverse, where good and evil are swapped - this gives these objects some mystique, which I think they deserve.
A visualization
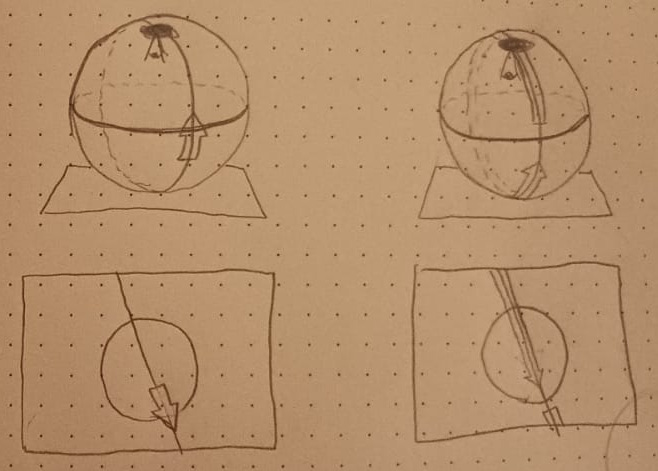
Below is a gif from a version of the animation program I’ve been working on. Here we are modifying a transformation represented by the arrow and axis. At the start you have a short arrow representing an ordinary translation. It can be twisted into being a rotation, and then twisted further into… something
Side by side:
So a nega translation goes off in some direction… infinitely far… passes through infinity, and then comes back from the other direction.
Yes, seriously. All the translations (“vectors”) you’ve thought about until now have been clockwise, using a sense of that word such that nega-translations are counter-clockwise. Another word for the quaternion clockwise/counter thing is “torque minimal route” and “torque maximal route”; for example one could go 90 degrees, the other would go -270 degrees. The equivalent here would be that an ordinary translation may have a distance of 3.5 meters; this kind of translation could have a distance of ∞-3.5 meters (or perhaps that should be 2∞-3.5…)
Maybe it even has a negative distance(/”displacement”)? Probably not. If you compose two nega translations, it flips back to being an ordinary translation. Compose three and you get a nega again, but surely if there were to be negative distance, it would increase in a regular way. Incidentally, a similar thing happens with “glide reflections”/transflections.
To back this up a little more I can appeal to stereographic projection, which has the ability to put all of euclidean space on the surface of a sphere (minus its north pole):
With stereographic projection, any straight line in euclidean space becomes a circle incident with the north pole. An ordinary translation is a directed arc you can slice from this circle; of course the related nega translation is the rest of that arc.
Nega translations are well-behaved enough to be worthy of attention
Reminder that in GA, we apply transformations (like rotations) to objects (like points, lines, planes and other transformations) using group conjugation:
What happens if M is a nega translation? Let’s cling to our algebraic security blanket for a bit:
…we see that applying -1-7e₀₃ is the same as applying 1+7e₀₃, the non-nega version. So both arcs of the infinite circle, the finite arc and the infinite arc, get you to the same place. This is what we might expect - and is seriously good to be assured of! Using the Dual Quaternion SLERP function, it is not impossible to actually get a nega translation, so thank goodness nothing weird happens.
This might lead you to believe nega translations will do the same thing as the non-nega (positive!) version in every situation. Nope! Time for the weird stuff.
Aside for very advanced readers: when applying Clifford algebra in physics, we usually apply two-sidedly but sometimes we apply one-sidedly. The above is two-sided application of a translation to a point, but I’ve found that with points specifically, you can work one-sidedly: (1+7e₀₃)e₁₂₃ will translate e₁₂₃ using (1+7e₀₃) just fine. Ok, ok, it’ll translate by half the distance it usually translates it, but that’s not a problem. The freaky part is that, with one-sided application, “applying” -1-7e and 1+7e to a point will have different effects; the nega translation will, unsurprisingly, give you the negative. This is to say, it “imparts” its orientation to the object, spinor-style rather than rotor-style.
2∞/2 = ∞?
Reminder: if you have two things in GA, in a general sense the thing that is an equal mixture of the two of them is their sum:
[10 degree rotation around e₁₂] + [30 degree rotation around e₁₂] = [20 degree rotation around e₁₂]
[e₁, planar reflection] + [e₁₂₃, point reflection] = [e₁+e₁₂₃, 90 degree rotoreflection]. Huh? Well, a planar reflection is a rotoreflection with an angle of 0 degrees; a point reflection is a rotoreflection with an angle of 180 degrees.
[0.8+0.6e₁₂, rotation by ~1.2 radians] + [1, the 0-degree rotation] = [rotation around e₁₂ by 0.6 radians], which is the “square root” of that rotation, the rotation around the same axis but with half the angle.
To say (3) more explicitly: a rotor’s (principle!) square root is that rotor plus 1, so long as the rotor is normalized*.
Gosh, nice formula! Warning that rotors actually multiple square roots; the formula just gives you a particular one, hence the “principle” - it’s like, “don’t take this formula too seriously, there are more serious linear algebra techniques for finding square roots”.
But if as a naieve newcomer you do apply the formula to a nega translation, the result is Borgesian existential horror:
The algebra is easy - but what’s the geometry? What is 7e₀₃?
7e₀₃ is one of the objects your teacher warned you about. “Work with k-reflections” we say, “Compose, i.e. multiply, invertible 1-vectors. Don’t just create objects additively; the Clifford group is the path, and the Clifford algebra is the forest full of wolves and hornets - there’s nothing for decent people to find there”.
As an element of geometry, e₀₃ is a line at infinity - not completely unreasonable. But as a transformation, it’s a translation by an infinite distance**. But hey, what did we expect? After all, -1+7e₀₃ takes you to infinity and back. We asked for its square root; we got a translation to infinity that leaves us there, with no way to make our way back to the proximity of the origin.
This creeps me out, not because it doesn’t make sense but because it does. I appreciate there’s nothing original about tweaking some formulae leads to infinities; but nobody told me that you can get directed, oriented infinities.
*A cheap way out of all of this would be to say that truly ”normalized” rotors cannot have a negative scalar part. I found that making this restriction lead to a bug somewhere in my codebase, but I can’t remember where. Another cheap solution is to say that the principle square root formula is normalize(1+normalize(M)) - this sees you reject the possibility that the result is 7e₀₃ because it would be divided it by 0. Debugging this was how I first encountered these beasts. I say this is all “cheap” because PGA is meant to be homogeneous; yes, normalization is useful, but there should be a norm-free version of everything you do.
**Actually, e₀₃ is only a translation by an infinite distance when applied single-sidedly - that will, for example, “translate” the origin to a point infinitely far in your translation’s direction. So what if you apply it double sidedly? That translates you by 2∞. The result is 0 because there’s nothing there. Listen to your teacher I guess.
Lotta logarithms
A rotation/translation/screw M has the general form scalar+bivector+quadvector. Logarithm(M) is a very useful and interesting bivector that essentially contains all the information you need on M. Certainly for PGA, the bible for the logarithm is NSELGA.
If you put a nega-translation into the NSELGA logarithm function, your program will crash because it’ll try to take a square root of a negative number. Sounds like a poor show by NSELGA, but it’s quite forgiveable - nega translations have the strange property of having multiple logarithms. This is unusual!

This said, while they have many logarithms in 3D PGA, they have no logarithm in 2D or 1D PGA. I suppose they have many more in 4D and up.
For the sake of completion, here’s another formula that tells you something about non-uniqueness of the logarithm; intuitively, it says “all 360 degree rotations are equivalent, no matter what line you go around”.
There is more structure to be explored relating to nega translations. I once saw someone say that they aren’t continuously connected to the identity - that’s false, they are (they just aren’t linearly connected to the identity, hence the square root insanity). What’s strange about them is that they are connected via screw motions - as you rotate and translate with a screw, you have brief moments where you have undergone a nega translation, then back to a screw, then a translation, then screw, then nega, etc. There’s more to this, relating to something called the Study Quadric, but I think it’s best to leave it here for now.
Addendum: is this The “Principle of Stationary Action”[butterfly meme]?
The Principle of Least Action is one of the most important things in all of applied mathematics. Oh, hey, beg your pardon - “Least” action is not what we’re supposed to say. We’re supposed to say stationary action.
What’s this clarification for? Apparently a path conforms to the PoSA if it minimizes or maximizes the action.
I wonder whether this is anything like what I’ve been talking about here - the translation is the minimal path, the nega-translation is maximal. Note that they’re both constrained and, together, they in some sense make up a geodesic.